Volume of a Conical Frustum Calculator

Conical Frustum Shape

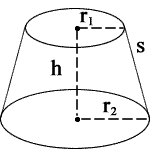
r₁ = radius1
r₂ = radius2
h = height
s = slant height
V = volume
L = lateral surface area
T = top surface area
B = base surface area
S = total surface area
π = pi = 3.14159
√ = square root

Calculate more with
Conical Frustum Calculator

Calculator Use

Online calculator to calculate the volume of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere and spherical cap.

Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft² or ft³. For example, if you are starting with mm and you know a and h in mm, your calculations will result with V in mm³.

Below are the standard formulas for volume.

Volume Formulas:

Capsule Volume

• Volume = πr²((4/3)r + a)
• Surface Area = 2πr(2r + a)

Circular Cone Volume & Surface Area

• Volume = (1/3)πr²h
• Lateral Surface Area = πrs = πr√(r² + h²)
• Base Surface Area = πr²
• Total Surface Area
  = L + B = πrs + πr² = πr(s + r) = πr(r + √(r² + h²))

Circular Cylinder Volume

• Volume = πr²h
• Top Surface Area = πr²
• Bottom Surface Area = πr²
• Total Surface Area
  = L + T + B = 2πrh + 2(πr²) = 2πr(h+r)

Conical Frustum Volume

• Volume = (1/3)πh (r₁² + r₂² + (r₁ * r₂))
• Lateral Surface Area
  = π(r₁ + r₂)s = π(r₁ + r₂)√((r₁ - r₂)² + h²)
• Top Surface Area = πr₁²
• Base Surface Area = πr₂²
• Total Surface Area
  = π(r₁² + r₂² + (r₁ * r₂) * s)
  = π[ r₁² + r₂² + (r₁ * r₂) * √((r₁ - r₂)² + h²) ]

Cube Volume

• Volume = a³
• Surface Area = 6a²

Hemisphere Volume

• Volume = (2/3)πr³
• Curved Surface Area = 2πr²
• Base Surface Area = πr²
• Total Surface Area= (2πr²) + (πr²) = 3πr²

Pyramid Volume

• Volume = (1/3)a²h
• Lateral Surface Area = a√(a² + 4h²)
• Base Surface Area = a²
• Total Surface Area
  = L + B = a² + a√(a² + 4h²))
  = a(a + √(a² + 4h²))

Rectangular Prism Volume

• Volume = lwh
• Surface Area = 2(lw + lh + wh)

Sphere Volume

• Volume = (4/3)πr³
• Surface Area = 4πr²

Spherical Cap Volume

• Volume = (1/3)πh²(3R - h)
• Surface Area = 2πRh

Triangular Prism Volume

\[ V = \dfrac{1}{4}h \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]