Right Triangles Calculator
Right Triangle Shape
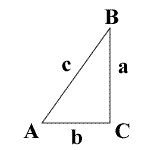
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c
K = area
P = perimeter
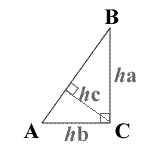
See Diagram Below:
ha = altitude of a
hb = altitude of b
hc = altitude of c
*Length units are for your reference only since the value of the resulting lengths will always be the same no matter what the units are.
Calculator Use
A right triangle is a special case of a triangle where 1 angle is equal to 90 degrees. In the case of a right triangle a2 + b2 = c2. This formula is known as the Pythagorean Theorem.
In our calculations for a right triangle we only consider 2 known sides to calculate the other 7 unknowns. For example, if we know a and b we can calculate c using the Pythagorean Theorem. c = √(a2 + b2). Once we know sides a, b, and c we can calculate the perimeter = P, the semiperimeter = s, the area = K, and the altitudes: ha, hb, and hc. Let us know if you have any other suggestions!
Formulas and Calculations for a right triangle:
- Pythagorean Theorem for Right Triangle: a2 + b2 = c2
- Perimeter of Right Triangle: P = a + b + c
- Semiperimeter of Right Triangle: s = (a + b + c) / 2
- Area of Right Triangle: K = (a * b) / 2
- Altitude a of Right Triangle: ha = b
- Altitude b of Right Triangle: hb = a
- Altitude c of Right Triangle: hc = (a * b) / c
1. Given sides a and b find side c and the perimeter, semiperimeter, area and altitudes
- a and b are known; find c, P, s, K, ha, hb, and hc
- c = √(a2 + b2)
- P = a + b + c
- s = (a + b + c) / 2
- K = (a * b) / 2
- ha = b
- hb = a
- hc = (a * b) / c
2. Given sides a and c find side b and the perimeter, semiperimeter, area and altitudes
- a and c are known; find b, P, s, K, ha, hb, and hc
- b = √(c2 - a2)
- P = a + b + c
- s = (a + b + c) / 2
- K = (a * b) / 2
- ha = b
- hb = a
- hc = (a * b) / c
For more information on right triangles see:
Weisstein, Eric W. "Right Triangle." From MathWorld--A Wolfram Web Resource. Right Triangle.
Weisstein, Eric W. "Altitude." From MathWorld--A Wolfram Web Resource. Altitude.