Calculators

Geometry

Plane

Equilateral Triangle Shape

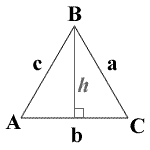
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c

A = B = C = 60°
a = b = c

K = area
P = perimeter
s = semiperimeter
h = altitude

*Length units are for your reference only since the value of the resulting lengths will always be the same no matter what the units are.

Calculator Use

An equilateral triangle is a special case of a triangle where all 3 sides have equal length and all 3 angles are equal to 60 degrees. The altitude shown h is hb or, the altitude of b. For equilateral triangles h = ha = hb = hc.

If you have any 1 known you can find the other 4 unknowns. So if you know the length of a side = a, or the perimeter = P, or the semiperimeter = s, or the area = K, or the altitude = h, you can calculate the other values. Below are the 5 different choices of calculations you can make with this equilateral triangle calculator. Let us know if you have any other suggestions!

Formulas and Calculations for a equilateral triangle:

• Perimeter of Equilateral Triangle: P = 3a
• Semiperimeter of Equilateral Triangle: s = 3a / 2
• Area of Equilateral Triangle: K = (1/4) * √3 * a²
• Altitude of Equilateral Triangle h = (1/2) * √3 * a
• Angles of Equilateral Triangle: A = B = C = 60°
• Sides of Equilateral Triangle: a = b = c

1. Given the side find the perimeter, semiperimeter, area and altitude

• a is known; find P, s, K and h
• P = 3a
• s = 3a / 2
• K = (1/4) * √3 * a²
• h = (1/2) * √3 * a

2. Given the perimeter find the side, semiperimeter, area and altitude

• P is known; find a, s, K and h
• a = P/3
• s = 3a / 2
• K = (1/4) * √3 * a²
• h = (1/2) * √3 * a

3. Given the semiperimeter find the side, perimeter, area and altitude

• s is known; find a, P, K and h
• a = 2s / 3
• P = 3a
• K = (1/4) * √3 * a²
• h = (1/2) * √3 * a

4. Given the area find the side, perimeter, semiperimeter and altitude

• K is known; find a, P, s and h
• a = √ [ (4 / √3) * K ] = 2 * √ [ K / √3 ]
• P = 3a
• s = 3a / 2
• h = (1/2) * √3 * a

5. Given the altitude find the side, perimeter, semiperimeter and area

• h is known; find a, P, s and K
• a = (2 / √3) * h
• P = 3a
• s = 3a / 2
• K = (1/4) * √3 * a²

For more information on triangles see:

Weisstein, Eric W. "Equilateral Triangle." From MathWorld--A Wolfram Web Resource. Equilateral Triangle.

Weisstein, Eric W. "Altitude." From MathWorld--A Wolfram Web Resource. Altitude.