Law of Cosines Calculator

Basic Calculator

Calculators

Geometry

Plane

Law of Cosines Calculator

Calculate:

Triangle Image

side a =

side b =

side c =

Angle Units

Length Units*

Significant Figures

Answer:

Primary Equation:

\[ A = \cos^{-1} \left[ \dfrac{b^2+c^2-a^2}{2bc} \right] \]
Sides:
a =
b =
c =

Angles:
A =
B =
C =

Other:
P =
s =
K =
r =
R =

Get a Widget for this Calculator

This Calculation Equation & Triangle

\( A = \cos^{-1} \left[ \dfrac{b^2+c^2-a^2}{2bc} \right]\)

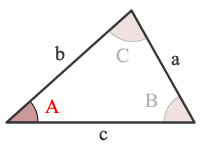
Triangle Diagram with Angles A, B and C and sides opposite those angles a, b and c respectively
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle

*Length units are for your reference-only since the value of the resulting lengths will always be the same no matter what the units are.

Calculator Use

Uses the law of cosines to calculate unknown angles or sides of a triangle. In order to calculate the unknown values you must enter 3 known values.

To calculate any angle, A, B or C, enter 3 side lengths a, b and c. This is the same calculation as Side-Side-Side (SSS) Theorem. To calculate side a for example, enter the opposite angle A and the two other adjacent sides b and c. Using different forms of the law of cosines we can calculate all of the other unknown angles or sides. This is the same calculation as Side-Angle-Side (SAS) Theorem.

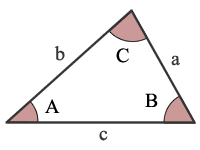
Law of Cosines

If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of cosines states:

\( a^2 = b^2 + c^2 - 2bc \cos A \)

\( b^2 = a^2 + c^2 - 2ac \cos B \)

\( c^2 = a^2 + b^2 - 2ab \cos C \)

Law of Cosines solving for sides a, b, and c

\( a = \sqrt{b^2 + c^2 - 2bc \cos A } \)

\( b = \sqrt{a^2 + c^2 - 2ac \cos B } \)

\( c = \sqrt{a^2 + b^2 - 2ab \cos C } \)

Law of Cosines solving for angles A, B, and C

\( A = \cos^{-1} \left[ \dfrac{b^2+c^2-a^2}{2bc} \right] \)

\( B = \cos^{-1} \left[ \dfrac{a^2+c^2-b^2}{2ac} \right] \)

\( C = \cos^{-1} \left[ \dfrac{a^2+b^2-c^2}{2ab} \right] \)

Triangle Characteristics

Triangle perimeter, P = a + b + c

Triangle semi-perimeter, s = 0.5 * (a + b + c)

Triangle area, K = √[ s*(s-a)*(s-b)*(s-c)]

Radius of inscribed circle in the triangle, r = √[ (s-a)*(s-b)*(s-c) / s ]

Radius of circumscribed circle around triangle, R = (abc) / (4K)

References/ Further Reading

Weisstein, Eric W. "Law of Cosines" From MathWorld-- A Wolfram Web Resource. Law of Cosines.

Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.

http://hyperphysics.phy-astr.gsu.edu/hbase/lcos.html

http://hyperphysics.phy-astr.gsu.edu/hbase/lsin.html